NMF应用场景
推荐
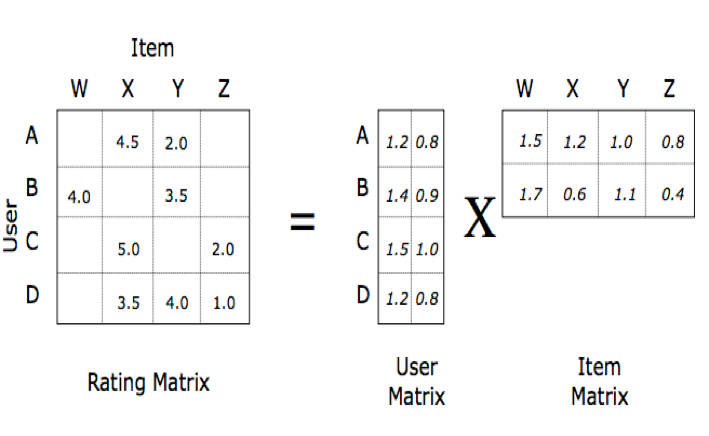
在推荐应用中,用户以及商品的历史关系相当于大型的矩阵,分解后的矩阵W以及H可以看成用户以及商品在兴趣维度的表达,根据分解后的矩阵可以预测未知的用户商品的打分情况。在Netflix竞赛中, Bellkor’s Pragmatic Chaos 采用该算法取得了 RMSE: 0.856704的好成绩,相比于原来的算法Cinematch效果提升了10.06%。
文本挖掘
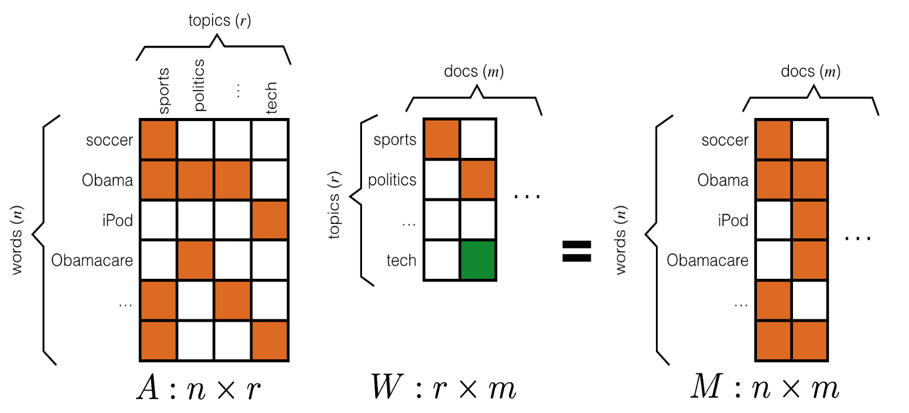
NMF可以看做LSI的近似算法,Document-Term矩阵的NMF分解结果可以看成是在topic空间对文档以及单词的低秩近似。利用NMF,一个文档是基础潜在语义的加法的组合,使得在文本域中更有意义。
交叉社区发现
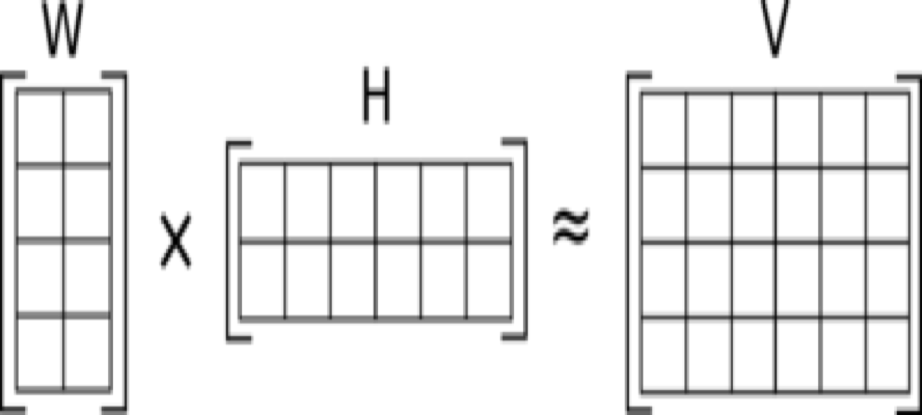
矩阵 $V$ 可以看作社交网络中用户关系矩阵。$W$ 中的 $k$ 个列向量看作新的特征空间下的一组基,$H$ 的每一行是在这组基下的新表示。因此,每个节点的表示向量 $x$ 可以用$W$的列向量的线性组合进行逼近$𝑥→𝑊ℎ^𝑇$,其中, $h$ 表示在各基向量的组合权重,代表节点到各个社区的隶属程度。
NMF理论推导
非负矩阵分解 (Nonnegative Matrix Factorization, NMF)是机器学习中重要的非监督学习算法,其广泛应用于话题发现和推荐系统等应用。给定一个非负样本矩阵(如$m$个用户对$n$个商品的打分矩阵)$\mathbf{R} \in R_{+}^{m \times n}$,NMF的目标为求解两个非负低秩矩阵$\mathbf{W} \in R_{+}^{m \times k}$,$\mathbf{H} \in R_{+}^{k \times n}$,最小化如下目标函数如下:
$$L\left ( \mathbf{W}, \mathbf{H} \right ) = \frac{1}{2} \left | \mathbf{R} - \mathbf{W}\mathbf{H^T} \right | + \frac{\lambda}{2}\left ( \left | \mathbf{W} \right |_F^2 + \left | \mathbf{H} \right |_F^2 \right )$$
其中$\left | . \right |$表示矩阵的F范数。上述目标函数也可以表示为:
$$L\left ( \mathbf{W}, \mathbf{H} \right ) = \frac{1}{2} \sum_{i = 1}^{m}\sum_{j = 1}^{n}\left ( r_{i,j} - w_i h_j^T \right ) + \frac{\lambda}{2}\left ( \left | \mathbf{W} \right |_F^2 + \left | \mathbf{H} \right |_F^2 \right )$$
其中$w_i$和$h_j$均为行向量,其分别对应矩阵$W$的第$i$个行向量和$H$的第$j$个行向量。可计算$W$和$H$的梯度如下:
$$\frac{\partial L}{\partial w_i} = -\sum_{j = 1}^{n}(r_{i,j} - w_i h_j^T)h_j + \lambda w_i = G_{w_i} + F_{w_i}$$
$$\frac{\partial L}{\partial h_j} = -\sum_{i = 1}^{m}(r_{i,j} - w_i h_j^T)w_i + \lambda h_j = G_{h_j} + F_{h_j}$$
其中,$G_{w_i} = -\sum_{j = 1}^{n}(r_{i,j} - w_i h_j^T)h_j$,$F_{w_i} = \lambda w_i$,$G_{h_j} = -\sum_{i = 1}^{m}(r_{i,j} - w_i h_j^T)w_i$,$F_{h_j} = \lambda h_j$。采用梯度下降的参数优化方式, 可得W以及H的更新方式见下式:
$$w_i \leftarrow \left [ (1 - \eta \lambda)w_i + \eta \sum_{j = 1}^{n}e_{i,j}h_j \right ]_+$$
$$h_j \leftarrow \left [ (1 - \eta \lambda)h_j + \eta \sum_{i = 1}^{m}e_{i,j}w_i \right ]_+$$
其中$\left [ x \right ]_+$定义为$\left [ x \right ]_+ = \left \langle max(x_1, 0),\cdots,max(x_k, 0) \right \rangle$。
实现
单机实现(Python)
下面是采用梯度下降(公式见上面)实现的NMF矩阵分解算法。
# coding=utf-8
import numpy as np
import math
import random
import argparse
# generate a matrix whose cell is in gauss distribution
def generate_gauss_dist_matrix(row, col, mu, sigma):
gauss_matrix = np.zeros(shape=(row, col))
for i in xrange(row):
for j in xrange(col):
gauss_matrix[i][j] = random.gauss(mu, sigma)
return gauss_matrix
# calculate gradients
def calculate_grad(user_lst, item_lst, rate_lst, row, col, matrix_w, matrix_h, prompt):
grad = np.zeros(shape=(row, col))
error_sum = 0 # calculate the the RMSE on train data.
for user, item, rate in zip(user_lst, item_lst, rate_lst):
eij = rate - np.dot(matrix_w[user, :], matrix_h[:, item])
error_sum += abs(eij)
if prompt == "W":
grad[user, :] += eij * matrix_h[:, item].T
else:
grad[:, item] += eij * matrix_w[user, :].T
return grad, error_sum
# update parameters
def update_paramters(row, col, matrix, grad, learn_rate, reg):
for i in range(row):
for j in range(col):
new = (1 - learn_rate * reg) * matrix[i][j] + learn_rate * grad[i][j]
matrix[i][j] = max(new, 0.0)
return matrix
def matrix_factorization_train(user_lst, item_lst, rate_lst, K=10, iters=100, learn_rate_init=0.001, reg=0.1):
max_user_id = max(user_lst)
max_item_id = max(item_lst)
sum_rate = sum(rate_lst)
count = len(user_lst)
# size
row = max_user_id + 1
col = max_item_id + 1
# matrix parameters distribution is gauss distribution.
print "initialization of the parameters......"
bias = sum_rate * 1.0 / count
mu = math.sqrt(bias / K)
sigma = 0.1
matrix_w = generate_gauss_dist_matrix(row, K, mu, sigma)
matrix_h = generate_gauss_dist_matrix(K, col, mu, sigma)
for iter in xrange(1, iters + 1):
learn_rate = learn_rate_init / math.sqrt(iter)
print "In this iteration, learn_rate is: " + str(learn_rate)
# update W
grad_w, error_sum = calculate_grad(user_lst, item_lst, rate_lst, row, K, matrix_w, matrix_h, "W")
matrix_w = update_paramters(row, K, matrix_w, grad_w, learn_rate, reg)
print "This is the " + str(iter) \
+ "th iteration after update W, and the RMSE of the Train data is " \
+ str(math.sqrt(error_sum * 1.0 / len(user_lst)))
# update Q
grad_h, error_sum = calculate_grad(user_lst, item_lst, rate_lst, K, col, matrix_w, matrix_h, "Q")
matrix_h = update_paramters(K, col, matrix_h, grad_h, learn_rate, reg)
print "This is the " + str(iter) \
+ "th iteration after update H, and the RMSE of the Train data is " \
+ str(math.sqrt(error_sum * 1.0 / count))
return matrix_w, matrix_h
def matrix_factorization_predict(user_lst, item_lst, rate_lst, matrix_w, matrix_h):
max_user_id = len(matrix_w)
max_item_id = len(matrix_h[0])
count = len(user_lst)
error = 0
for user, item, rate in zip(user_lst, item_lst, rate_lst):
# filter the triple whose user or item are not trained.
if user >= max_user_id or item > max_item_id:
continue
error += abs(rate - np.dot(matrix_w[user, :], matrix_h[:, item]))
rmse = math.sqrt(error / count)
return rmse
# Return the user_lst, item_lst, rate_lst of the movie info.
def load_data(file_pt):
user_lst = list()
item_lst = list()
rate_lst = list()
with open(file_pt) as f:
for line in f:
try:
fields = line.strip().split()
user_lst.append(int(fields[0]) - 1)
item_lst.append(int(fields[1]) - 1)
rate_lst.append(int(fields[2]))
except ValueError:
print "format must be [user, item, rate, *]!"
return user_lst, item_lst, rate_lst
def parse_args():
parser = argparse.ArgumentParser(description="NMF demo by Ping Li")
# optional args
parser.add_argument("-l", "--learn_rate", type=float, metavar="\b", default=0.001, help="learn rate, default 0.001")
parser.add_argument("-r", "--reg", type=float, metavar="\b", default=0.1, help="reg, default 0.1")
parser.add_argument("-i", "--iter", type=int, metavar="\b", default=50, help="iter num, default 50")
parser.add_argument("-K", "--K", type=int, metavar="\b", default=10, help="iter num, default 10")
# necessary args
parser.add_argument("-tr", "--train_pt", metavar="\b", help="train data path", required=True)
parser.add_argument("-te", "--test_pt", metavar="\b", help="test data path", required=True)
args = parser.parse_args()
if args.learn_rate < 0.0 or args.reg < 0.0 or args.iter < 0 or args.K < 0:
raise ValueError("learn_rate, reg, iter, K must be positive")
return args
if __name__ == "__main__":
args = parse_args()
train_user_lst, train_item_lst, train_rate_lst = load_data(args.train_pt)
test_user_lst, test_item_lst, test_rate_lst = load_data(args.test_pt)
print "NMF train start......"
# A descent parameters for NMF.
W, H = matrix_factorization_train(train_user_lst, train_item_lst,
train_rate_lst, args.K, args.iter, args.learn_rate, args.reg)
print "NMF test start ......"
rmse = matrix_factorization_predict(test_user_lst, test_item_lst, test_rate_lst, W, H)
print "RMSE of the matrix factorization on test data is " + str(rmse)
# command line
# python NMF.py --learn_rate 0.001 --reg 0.1 --iter 100 -K 10 --train_pt "./u1.base" --test_pt "./u1.test"
实现要点
参数初始化
由于 NMF 是一个非凸问题,所以只能找到一个 local optimal。参数初始值的选取对结果的影响比较大。参数初始值最好离预期解比较近,所以其重构后应尽可能和原样本值接近:
$$w_i h_j = R_{i,j}$$
一种简单的策略是让参数随机初始值重构后的值等于 $R$ 的均值 $\mu$:
$$W = DenseMatrix(m, K) \times \sqrt{\frac{\mu}{K}}$$
$$H = DenseMatrix(K, n) \times \sqrt{\frac{\mu}{K}}$$
RMSE震荡问题
在优化的过程中,如果在迭代过程一直保持一个学习率会导致loss震荡,在优化的过程中步长宜逐渐减小。
$$learnrate = \frac{lr} { math.sqrt(step)}$$