背景
在Spark分布式计算框架下,机器学习算法有两种分布式实现方式:数据分布和模型分布。数据分布将数据集无差别地划分为多个数据子集,然后将数据子集分发到集群的各个节点上进行并行处理,并在每个节点上保留一份完整的模型参数,在参数完成局部更新之后,需要汇合每个节点上的局部参数值得出全局参数值。 Spark MLlib中大部分算法采用了数据分布实现。与数据分布中每一个计算节点都需要保留一份完整的模型参数不同,模型分布同时将数据和参数分发到各个节点上进行处理,因而能够支持更细粒度的并行化。机器学习算法库GraphLab将数据和模型构成一个有向无环二部图采用模型分布与异步通信的方式对算法进行迭代计算。
相比较而言,数据分布算法实现相对简单,通信代价小,但其要求在每一个节点上都保存一份完整的模型参数,因而难以满足具有大规模参数的机器学习算法的训练;采用模型分布的机器学习算法实现比较复杂,需要将训练样本与模型参数的关系抽象出一个二部图,每一个样本与模型参数都是图上的节点,同时由于数据和模型参数都分布在不同的计算节点上,因此训练过程中的通信开销较大,但其主要优势在于可以支持大规模参数的模型训练。
数据分布
数据分布介绍
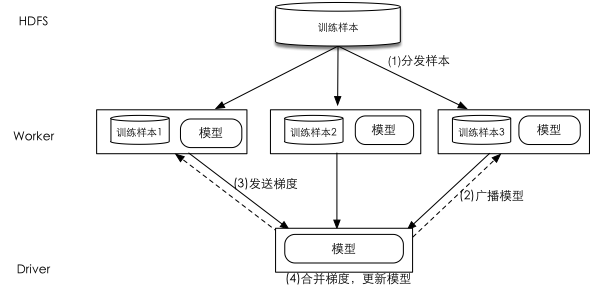
数据分布是将训练数据进行划分并分发到不同节点以实现算法并行的一类方式的统称。图-1是Spark 环境中采用数据分布实现并行算法的示意图:(1)Driver将训练样本分成若干个分区分发到各个Worker上; (2)Driver向所有的Worker广播模型参数;(3)每一个Worker根据当前的模型和所拥有的本地局部数据计算出梯度并将其发送给Driver;(4)Driver接收到所有Worker的梯度后将其合并并对现有的模型参数进行更新。算法重复步骤(2)-(4)直至收敛。
数据分布式在各种分布式机器学习算法库中被广泛采纳,例如Spark中重要的机器学习算法库MLlib采取数据分布的方式实现不同的机器学习算法,基于Hadoop MapReduce分布式架构实现的大规模数据挖掘与机器学习库Mahout也是采用的数据分布。
以LR为例介绍数据分布
Logistic Regression 算法可以看成对一个正则化后的负对数似然函数的优化过程,在二值分类问题中,假设给定$N$个训练样本,$x_i$为第$i$个样本的K维特征向量,为第$i$个样本的标签,$t_i = 0$表示第$i$个样本为负例,$t_i = 1$表示其为正例。进一步假设预测模型为线性函数,即$f\left ( x \right ) = \left \langle \mathbf{w, x} \right \rangle + b$,其中和为模型参数。Logistic Regression的目标函数由经验风险项和$l$2正则项组成:
(1)$$L \left (\mathbf{w} \right ) = - \sum_{i = 1}^N \left [ t_i ln \left ( y_i \right ) - \left ( 1- t_i \right ) ln\left ( 1 - y_i \right ) \right] + \frac{\lambda }{2}\left | \mathbf{w} \right |_2^2$$
其中为使用模型对第i个样本的预测值,为平衡经验风险与正则项的系数。Logistic Regression的目标函数可以采用梯度下降法(GD:Gradient Descent)进行优化,根据(1)式,可求得b以及w的梯度如下:
(2) $$\frac{\partial L}{\partial b} = - \sum_{i = 1}^N\left ( t_i - y_i \right ) = G_b$$
(3) $$\frac{\partial L}{\partial b} = - \sum_{i = 1}^N\left ( t_i - y_i \right ) \times x_i + \lambda \mathbf{w}= G_{\mathbf{w}} + \mathbf{F}$$
为了便于并行化,将对w的梯度分成两部分,其中$G_\mathbf{w} = - \sum_{i = 1}^N\left ( t_i - y_i \right ) \times x_i$, $F = \lambda \mathbf{w}$。
采用GD参数优化方式, 可得w以及b的更新方式如下:
(4) $$b\leftarrow b + \eta \sum_{i = 1}^N\left ( t_i - y_i \right )$$
(5) $$\mathbf{w}_j \leftarrow \left ( 1 - \eta \lambda \right )\mathbf{w}_j + \eta \sum_{i = 1}^N\left ( t_i - y_i \right ) x_i^j,for j = 1,\cdots, K$$
其中为预设的学习步长。
算法1展示了使用数据分布实现Logistic Regression算法的伪代码,其在算法执行初始将训练样本$S$划分成多份并分发到不同的计算节点上,并广播模型参数w和b到所有的计算节点。在每一次迭代过程中,首先每一个计算节点根据本地的数据和当前参数值$\mathbf{w}$和$b$计算本地的梯度$G_{\mathbf{w}}^i$和$G_b^i$;然后集群的Driver节点聚合所有计算节点上梯度$G_{\mathbf{w}}^i$和$G_b^i$,更新全局的参数值,并向所有的计算节点进行广播;计算节点在接收到更新后的全局参数值后,开始下一轮的迭代。

数据分布一般形式
数据分布的一般流程图见下图。首先挖掘出算法中可以并行的部分在Worker中运行,在以梯度下降为优化算法的机器学习算法中,计算梯度是明显可以并行的部分,在灰色节点中执行;相反合并梯度广播参数等这些操作在黄色节点Driver中执行。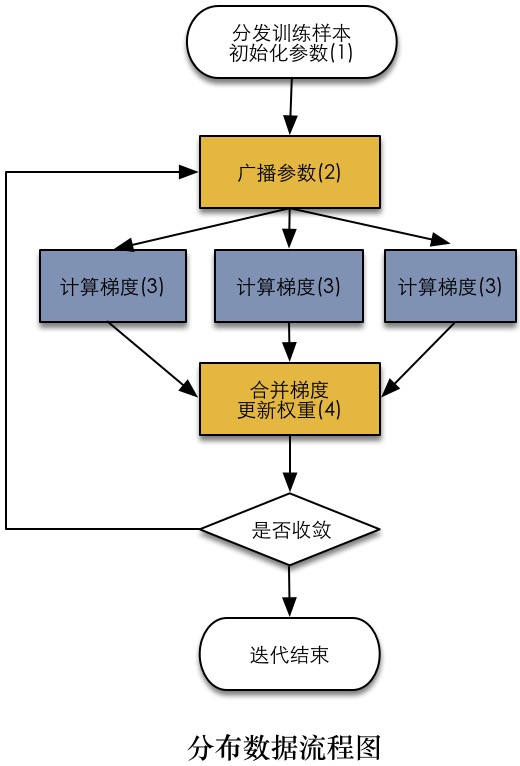
模型分布
模型分布介绍
模型分布是将模型参数分布在不同的节点实现分布式计算的一类方式的统称。使用模型分布实现分布式机器学习算法,首先要构建一个二部图,如图-2所示,其中为样本顶点表示每一个输入的训练样本,为参数顶点表示模型中每一个参数。用表示样本对参数关联程度(在线性模型假设下,为样本的第j维特征),当时,顶点与顶点之间建立起权重为的边,反之,顶点与顶点之间没有边。
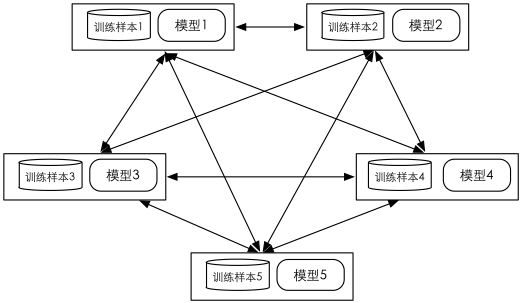
图-3为基于Spark的GraphX[9]采用模型分布实现并行算法的示意图:(1)通过GraphX将二部图的分布式存储到不同的Spark计算节点;(2)模型顶点向与其邻接样本顶点发送模型参数信息;(3)样本顶点计算该样本上的梯度并发送给邻接的参数顶点;(4) 参数顶点在接受到梯度信息后更新自身权重。重复(2)-(4)直至收敛。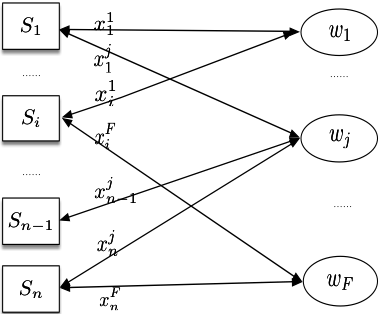
以LR为例介绍模型分布
与数据分布的实现方式不同,模型分布需要首先根据模型参数和训练样本构造二部图, 在Logistic Regression中顶点与顶点分别代表第$i$个样本和第$j$个参数,当$x_i^j \neq 0$时,顶点$S_i$与顶点$\mathbf{w}_j$之间会有权重为的边,反之,顶点$i$与顶点$j$之间没有边。 算法2展示了使用模型分布式实现Logistic Regression算法的伪代码,在对此二部图划分和分发后算法开始对模型参数进行迭代更新,在每一轮迭代中,首先每一个参数顶点将其参数值发送给其相邻的样本顶点,各个样本顶点根据接收到的参数值计算当前模型的预测值以及梯度向量,并向其相邻的参数顶点广播其得到的梯度向量。参数顶点接收到所有的梯度向量后进行梯度聚合和参数更新,完成一轮迭代过程。
模型分布一般形式
模型分布的一般流程图见下图。首先应该构造出样本到模型的二部图,如上图所示,因为在模型分布的过程中数据与模型都是作为二部图中的顶点存储在不同的计算节点上,所以各个步骤都无差地在计算节点上运行,如下图所示。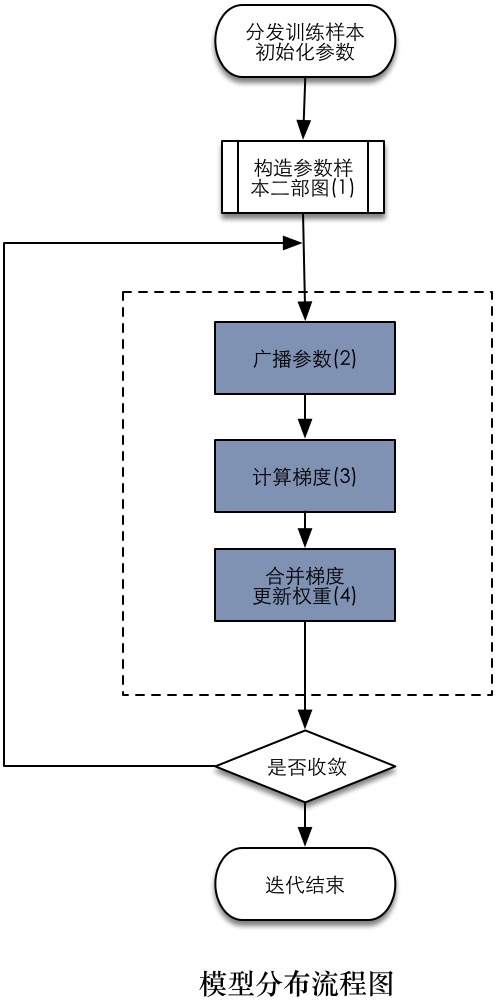
应用场景
- 从编程方式来看,数据分布因为模型以广播的形式分发,编程较简单。
- 从可扩展性来看,模型分布因为模型参数可以分布式存储,具备支持大规模模型训练的能力。
- 从计算效率来看,模型分布可以更好地解决模型规模大、单个节点无法存储的问题,适合基于大规模但稀疏的数据训练机器学习模型;在数据规模小或非稀疏的情况下,使用数据分布方式通信开销小,可以加速模型训练。