Pagerank 幂法实现

Graphx中Pagerank中的不足

  前一段时间为了完善bda studio中得算法，我调研了spark graphx中的pagerank，之后就萌发了要自己重写pagerank的想法。开始想重写pagerank完全是因为当初固执地想让一个算法收敛，而不是给定一个最大迭代次数，让算法终止，因为这样算法究竟收敛不收敛心里很没有底气。当我测试完spark graphx中得pagerank以后，发现了很多问题，这更加坚定了我写好这个算法的心。在这里提一句，我测试该算法使用的是twitter数据集的两个文件，分别是twitter_rv.net以及numeric；前者是边文件，后者是用户id以及用户名字典，这个数据集边大概有10亿左右，顶点有四千万。graphx的pagerank算法写的虽然十分简短精炼，但是存在着这样两个问题：

• 收敛性方面：算法迭代的时候pagerank值在不断的变化，总的pagerank值也在不断变小，这也说明无论迭代多少次，这样的算法也是不可能收敛的，因为迭代次数越多，损失的pagerank值也越多。
• 效率方面： 该算法在迭代的时候，迭代时间变得越来越长, 迭代时间几乎成倍增长，如果该算法整体的迭代次数比较短还可以忍受，但是越到后来迭代时间会达到一个小时左右，有时候会造成内存崩溃。

幂法跟传统pagerank的根本区别

  在一个网络图中，经常会出现出度为0 的顶点，如上图顶点C，如果仍然用之前的方式，即所有顶点以damping factor的概率沿着链接跳转，(1 - damping factor)的概率随机访问，那么每次迭代就会损失所有出度为0的顶点的pagernak总和乘以damping factor。简而言之，就是这些出度为0 的顶点有85%(默认damping factor就是0.85)的pagerank并没有给其他的顶点。

  那怎样才是合理的呢，从经验上讲，对于这些出度为0的顶点，它们应该将自己100%的pagerank随机地贡献给所有的页面才是合理的。也就是说，当没有链接往下跳转的时候，我们随机地选择任意一个网页。幂法跟传统的pagerank最根本的区别就是合理地处理了出度为0的顶点的pagerank值，让迭代的过程pagerank总和不变，只是各个网页的pagerank值有增有减。

算法介绍

  假设$N$是Internet 中所有可访问的网页的数目，此数值非常大，定义：$N \times N$的网页链接矩阵$G = g_{i,j}\in R^{N*N}$, 若网页i存在链接到j, 则有$g_{i,j} = 1$, 否则 $g_{i,j} = 0$。大规模稀疏矩阵有如下特点：

• G中非零元素的的数目是整个Internet中超链接的数目。
• 第j列非零元素的位置表示了所有链接到网页j的网页。
• 第i行非零元素的位置表示了所有从网页i链接出去的网页。
• 记矩阵行元素之和 $r_i = \sum _j g_{i,j}$, 它表示了第i个网页的出度。
• 记矩阵列元素之和 $c_j = \sum _i g_{i,j}$, 它表示了第j个网页的入度。

  要计算pagerank, 可假设一个随机上网“冲浪”的过程，即每次看完网页后有两种选择：

  在当前网页中随机选择一个超链接进入下一个网页。
随机打开一个新的网页。
  设$p$为从当前网页上找一个链接跳转过去的概率(也叫damping factor)，则$1 - p$即为不选当前网页链接，随机去任意一个网页的概率。若当前网页是 $i$，则其跳转到网页 $j$ 的可能性有两种：

• 网页 j 在网页 i 的链接上，也就是说这两个顶点之间存在有向边，其概率为 $\frac {p}{r_i} + \frac {1 - p}{N}$.
• 网页 j 不在网页 i 的链接上，也就是说这两个顶点不存在有向边，其概率为 $\frac {1 - p}{N}$.
• 由于网页 i 与网页 j 之间是否存在有向边由$g_{i,j}$决定，则转移矩阵为：

$$a_{i,j} = p \times \frac{g_{i,j}}{r_i} + \frac{1 - p}N$$

  需要注意的是，如果 $r_i = 0$, 则意味着 $g_{i,j} = 0$, 上式中 $a_{i,j} = \frac{1}{N}$。任意两个网页之间的转移矩阵 $A = \left(a_{i,j} \right)_{n \times n}$。设矩阵D为各个网页出度的倒数(若没有出度则置为1)构成N阶对角矩阵, $e$是全为1的N维向量, 则有：

$$A = pGD + \frac {1 - p}{N}ee^T $$

  设 $x_i ^k$, i = 1,2,3…n表示某时刻 k 网页 i 的pagerank值, 向量 $x^k$表示当前时刻各个网页的pagerank。那么下一时刻浏览到网页 j 的概率为 $x_j^ {k + 1} = \sum_i a_{i,j} \times x_i^k$, 此时浏览网页的pagerank为 $x^{k + 1}= Ax^k$.

  当这个过程无限进行下去，达到极限情况，即网页访问概率 $x^k$ 收敛到一个极限值，这个极限向量x为各个网页的pagerank，它满足 $Ax = x$, 且 $\sum_i^n x_i = 1 $. 最后可以看出求得的pagerank实际上也是矩阵A在特征值为1时的特征向量。

Spark Graphx 实现

  将每个节点的pagerank值分成两部分，第一部分是通过链接跳转过来的，第二部分为不通过链接跳转的部分。贡献第二部分的pagerank值的节点有两类：

出度为 0 的顶点，这些顶点以1/N的概率跳转到其他页面, 对任意一个网页的贡献为$\frac{x_i}{N}$；
出度不为 0 的顶点，这些顶点以(1 - p) / N的概率跳转到其他网页，贡献了$\frac {(1 - p) \times x_i}{N}$;
由于第二部分得到的pagerank对所有的节点而言都是一样的，在graphx中，计算第一部分使用消息传递，第二部分可以采用map操作。

如何解决迭代时间变长

  迭代时间变长是由于RDD的lazy computation的特性，以及RDD为了错误恢复，在迭代的过程中都保留着很长且复杂的依赖关系(lineage dependency)，不过为什么lineage越长会造成迭代时间越长，揣测是因为迭代的时候会占用大量内存，这也是为什么迭代次数太多会发生内存泄露。解决这个问题，主要就是要懂得合理的cache以及unpersist, 仅仅这些还不够，还需要在适当的时候，truncate lineage设置checkpoint。

  下面是我train pagerank的代码：

/** Update the vertex with new pagerank.*/
def updateVertex(id: VertexId, attr: Double, msg_sum: Double): Double = {
  damping_factor * msg_sum
}

def sum(a: Double, b: Double): Double = a + b

/** Send pr/out_degree with edge direction.*/
def sendPR(e: EdgeContext[Double, Double, Double]) = {
  e.sendToDst(e.srcAttr * e.attr)
}
  /**
   * Run pagerank algorithm with damping_factor and max_iter.
   * @param g The original graph.
   * @return An RDD includes all vertices' id and pagerank value.
   */
  def run(g: Graph[Double, Double]): PagerankModel = {
    N = g.vertices.count()
    //Cache the outdegree to get the vertices whose outdegree is 0.
    val outdegree = g.outDegrees.cache()

    //Initialize the graph with its pr set 1/N and edge attr set 1/out_degree
    var graph = g.outerJoinVertices(outdegree) {
      case (vid, vdata, deg) => deg.getOrElse(0)
    }.mapTriplets(e => 1.0 / e.srcAttr)
      .mapVertices((id, attr) => 1.0 / N)
      .cache()

    // v is a vertices set whose outdegree is > 0.
    val v: VertexRDD[Double] = graph.vertices.innerJoin(outdegree) { (vid, PR, deg) => PR }
    // special_vertices are vertices whose outdegree is 0.
    val special_vertices = graph.vertices.subtract(v).cache()
    special_vertices.checkpoint()
    outdegree.unpersist(blocking = false)

    //send messages:[ pr / out_degree ].
    //aggregate messages to the same dstId.
    var messages: VertexRDD[Double] = graph.aggregateMessages(sendPR, sum).cache()
    var old_message: VertexRDD[Double] = null

    //K is the num of vertices whose out_degree is 0.
    K = N - outdegree.count()
    //Respectly calculate the avg_PR_deg1 for pages with out_degree
    //and avg_PR_deg0 for pages with out_degree 0.
    var avg_PR_deg1 = (1.0 - K * 1.0 / N) / N
    var avg_PR_deg0 = 1.0 * K / (N * N)

    var preG: Graph[Double, Double] = null
    val times = new ArrayBuffer[Double]()
    var iter = 0
    while (iter < max_iter) {
      val timer = new Timer()
      val new_PR: VertexRDD[Double] = graph.vertices
        .innerJoin(messages)(updateVertex).cache()
      preG = graph

      //update tht pagerank value.
      graph = graph.outerJoinVertices(new_PR) {
        case (vid, old_PR, new_opt) => new_opt.getOrElse(0.0)
      }.mapVertices {
        (id, PR) => PR + avg_PR_deg1 * (1 - damping_factor) + avg_PR_deg0
      }.cache()
      graph.vertices.foreachPartition(f => {})
      graph.checkpoint()

      old_message = messages
      messages = graph.aggregateMessages(sendPR, sum).cache()

      //all pagerank value sum.
      val sum_PR: Double = graph.vertices.map { case (id, attr) => attr }.sum()
      //pagerank sum for those vertices whose outdegree is 0.
      val sum0_PR = graph.vertices.innerJoin(special_vertices) {
        case (id, pr, zero) => pr
      }.map {
        case (id, attr) => attr
      }.sum()

      avg_PR_deg1 = (sum_PR - sum0_PR) / N
      avg_PR_deg0 = sum0_PR / N

      iter = iter + 1
      val cost_time = timer.cost()
      times.append(cost_time)
      val msg = Msg(s"iter " -> iter, s"cost_time(ms)" -> cost_time)
      logInfo(msg.toString)

      old_message.unpersist(blocking = false)
      preG.unpersist(blocking = false)
      new_PR.unpersist(blocking = false)
    }
    val avg_time = times.sum / iter
    logInfo(s"average iteration time is: $avg_time ms.\n")
    val PR: RDD[(VertexId, Double)] = graph.vertices
    val prmodel = new PagerankModel(PR)
    prmodel
  }

总结

  pagerank还是一个收敛很快得算法，对于上面测试的社交网络图，规模还是很大的，迭代15次以后，top50的users 基本跟某一篇论文中次序完全一致。在效果方面，如果只要保证topK用户的次序，迭代次数不用很多；在效率上看，如果图不是很大，设置checkpoint可以不用那么频繁，比如迭代两三次写一次hdfs也行，另外在spark对图进行partition的过程中，应尽量减少通信，也就是说有同样srcID的被分到同一个partition中，spark Graphx中有相应的API，PartitionStrategy.EdgePartition2D。

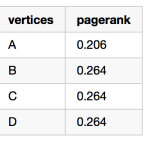
  上图中的pagerank分别为：